Understanding Binary, Hexadecimal, and Octal Literals in Java

When you write numbers in Java, you're usually working with the decimal system (base-10). But Java also supports binary (base-2), hexadecimal (base-16), and octal (base-8) number systems. These systems are not just for computer scientists or hardware engineers. They're essential in many areas of programming, especially when working with bit-level operations, low-level systems, or even things like file permissions and color codes.

Whether you're building embedded applications, working with bitmasks, or just want to understand how values are stored in memory, knowing how to interpret and write values in different number systems is a fundamental skill.

In this article, we'll break down what binary, hexadecimal, and octal systems are, how to convert between them, and how to use them directly in Java using simple syntax like 0b, 0x, and 0.

🔢 What Are Binary, Hexadecimal, and Octal Systems?

Let's briefly understand these number systems and how they differ from the decimal system:

1. Binary (Base-2)

• Uses only two digits: 0 and 1
• Every digit represents a power of 2
• Common in bitwise operations, hardware-level programming
• Mirrors how computers represent data using ON/OFF (1/0) electrical states

Example: Binary 1010 = 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 10 (in decimal)

2. Hexadecimal (Base-16)

• Uses digits 0-9 and letters A-F (or a-f)
• A = 10, B = 11, …, F = 15
• Commonly used in memory addresses, bit masks, color codes
• One hex digit represents exactly 4 binary digits (bits), which maps neatly to bytes

Example: Hex 1A = 1*16^1 + 10*16^0 = 16 + 10 = 26 (in decimal)

3. Octal (Base-8)

• Uses digits from 0 to 7
• Each digit represents a power of 8
• Sometimes used in UNIX file permissions

Example: Octal 123 = 1*8^2 + 2*8^1 + 3*8^0 = 64 + 16 + 3 = 83 (in decimal)

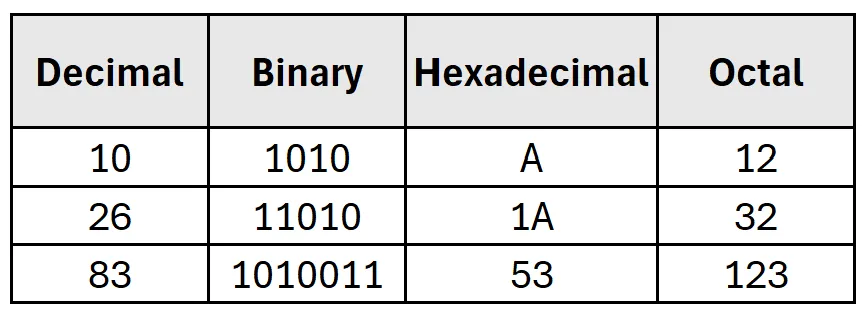
📊 Quick Reference Table

Quick Comparison of Decimal, Binary, Hexadecimal, and Octal Representations

💡 How to Represent These in Java

Java provides special syntax to represent numbers in these systems directly in code:

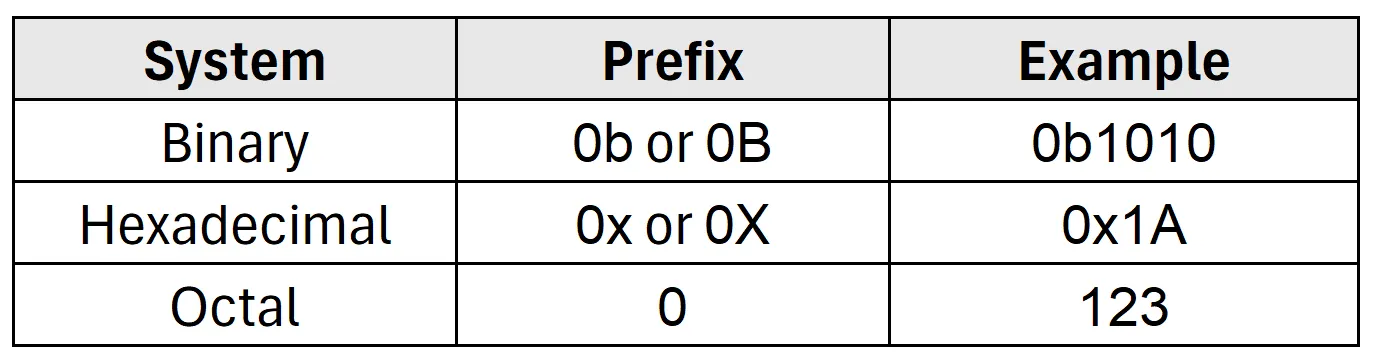
These literals can be assigned to any integral types like byte, short, int, or long as long as they fall within the valid range for that type.

Note: Binary literals using 0b or 0B were introduced in Java 7, while hexadecimal (0x or 0X) and octal (0) literals have been supported since the earliest versions of Java, including Java 1.0.

💻 Java Code Example

Here's a simple Java program that demonstrates number literals in binary, hexadecimal, and octal:

public class NumberLiteralBasicsDemo {
    public static void main(String[] args) {
        int binary = 0b1010;
        System.out.println("Binary 0b1010 = " + binary);
        int hex = 0x1A;
        System.out.println("Hexadecimal 0x1A = " + hex);
        int octal = 0123;
        System.out.println("Octal 0123 = " + octal);
    }
}

📂 Want to See These in Action?

For complete, practical examples demonstrating how binary, hexadecimal, and octal literals can work with various data types (byte, short, int, long), check out the following Java programs on GitHub:

🔗 BinaryLiteralDemo.java
🔗 HexadecimalLiteralDemo.java
🔗 OctalLiteralDemo.java

👉 Explore the full repository here: mastering-java on GitHub

🔁 Step-by-Step: Manually Converting Decimal to Binary, Hexadecimal, and Octal

📌 Visual Tip: You can visualize the decimal to binary conversion as a binary tree, where each level represents a power of 2:

        8
       / \
      4   0
     / \
    2   0
   / \
  1   0

Each '1' in binary represents a path where a power of 2 is used. So, for decimal 10 → binary 1010 = 8 + 2.

✅ Decimal to Binary

Divide the number by 2, record the remainder, and continue dividing the quotient until you reach 0. Reverse the remainders.

Example: Convert 10 to binary

10 / 2 = 5, remainder = 0
5 / 2 = 2,  remainder = 1
2 / 2 = 1,  remainder = 0
1 / 2 = 0,  remainder = 1
=> Binary = 1010

✅ Decimal to Hexadecimal

Divide by 16 and use 0–9, A-F.

Example: Convert 26 to hex

26 / 16 = 1, remainder = 10 (A)
1 / 16 = 0,  remainder = 1
=> Hex = 1A

✅ Decimal to Octal

Divide by 8 and reverse:

Example: Convert 83 to octal

83 / 8 = 10, remainder = 3
10 / 8 = 1,  remainder = 2
1 / 8 = 0,   remainder = 1
=> Octal = 123

🧠 When to Use These Literals in Java

• Binary: Useful in bit manipulation, flags, and masks (e.g., 0b00001111)
• Hexadecimal: Great for working with color codes, memory addresses, or compact bit-level configurations
• Octal: Less common, but used in file permission settings (e.g., 0755)

Fun fact: Many developers use hexadecimal color codes like #FF5733 in web development. In Java, that's 0xFF5733!

⚠️ Common Mistakes to Avoid

1. Leading 0 ≠ decimal:

• 0123 is not 123 in decimal; it's octal and equals 83.

2. Don't use commas in numeric literals:

• int x = 1,000; → ❌ Syntax error
• ✅ Use underscores instead: int x = 1_000;

3. Case doesn't matter for 0x or 0b:

• 0X1A and 0x1A are both valid

🤔 Did You Know?

In early Unix systems, file permissions were represented using octal values. For example:

• chmod 755 sets permissions to rwxr-xr-x
• This maps to octal: 7 (rwx), 5 (r-x), 5 (r-x)

This is why octal notation (with a leading 0) is still relevant today in many system-level and DevOps scripts.

🎯 Final Thoughts

Understanding number systems like binary, hexadecimal, and octal isn't just academic, it has real-world applications in programming. Java makes it easy to work with these formats using simple prefixes. Whether you're dealing with low-level data, debugging binary flags, or defining bitmasks, knowing how to represent and convert these values is a valuable skill.

Play around with them in your own Java programs. Try building a mini tool that takes a decimal input and outputs its binary, hexadecimal, and octal equivalents using Integer.toBinaryString(), Integer.toHexString(), and Integer.toOctalString().

It's a great way to sharpen your fundamentals and understand what's happening under the hood.

Let me know in the comments if you'd like a follow-up on bitwise operations using these literals, like how to use &, |, ^, and ~ for real-life scenarios!